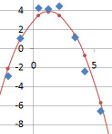
 Поводом для написания этой заметки стала беседа с коллегой по работе, который сделал измерения двух взаимосвязанных величин, нанес их на плоскость и заметил, что они напоминают часть параболы. Он попросил найти аппроксимацию, максимально близко располагающуюся около точек измерения.
Поводом для написания этой заметки стала беседа с коллегой по работе, который сделал измерения двух взаимосвязанных величин, нанес их на плоскость и заметил, что они напоминают часть параболы. Он попросил найти аппроксимацию, максимально близко располагающуюся около точек измерения.
Предположим мы сделали несколько не очень точных измерений каких-то двух, скорее всего взаимосвязанных физических величин и результаты нанесли на плоскость в виде точек. Эти результаты на плоскости напоминают какую-то кривую, возможно параболу, как же ее найти?
Решение.
Запишем уравнение параболы в виде:
А результаты изменений произвольно пронумеруем и занесем в таблицу:
| Номер измерения i | Результат измерения величины x | Результат измерения величины y |
| 1 | x1 | y1 |
| 2 | x2 | y2 |
| … | … | … |
| N | xN | yN |
Нумерация точек может быть произвольной, главное сохранить пары точек .
Для удобства данные можно занести в Microsoft Excel
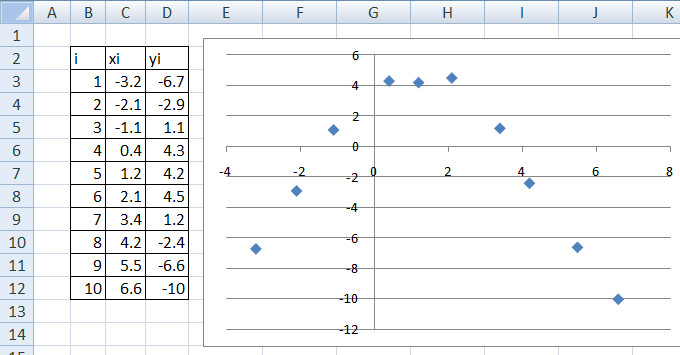
Файл с данным примером в формате Excel можно скачать тут: Data.xls.
Данные подготовлены. А что дальше? Как найти параметры параболы , располагающейся максимально близко ко всем точкам одновременно? Понятно, что если количество точек больше трех и точки имеют случайную составляющую (или попросту говоря шум измерения) провести параболу через все точки одновременно в общем случае невозможно.
На языке математики указать, что точка с номером должна быть максимально близко к параболе можно так:
Для того чтобы указать на то, что бы все точек оказаться максимально близко к параболе можно воспользоваться выражением:
Которое обозначает что сумма квадратов «несоответствия» всех точек должна быть минимальна. В этом и заключается суть Метода Наименьших Квадратов (МНК), по-английски метод называется the Method of Least Squares. Данный метод можно назвать основным для обработки статистических данных и определения корреляции.
Последнее выражение фактически обозначает, что если каким-то образом можно подобрать коэффициенты так, чтобы сумма
окажется минимальной, то задача будет решена. Можно найти коэффициенты
простым перебором или угадать, можно применить какие либо иные, более или менее эффективные численные методы, а можно найти точное аналитическое решение.
Выберем последний путь, так как он позволяет получить наиболее точное решение при минимуме вычислительных затрат.
Из математического анализа известно, что минимум функции находится в точке, где производная этой функции равна нуля. Наша функция зависит от трех параметров и не может быть отрицательной, так как под суммой выражение в квадрате. Найдем частные производные от
по
и приравняем каждую из них к нулю. Получим три уравнения которые должны быть решены совместно:
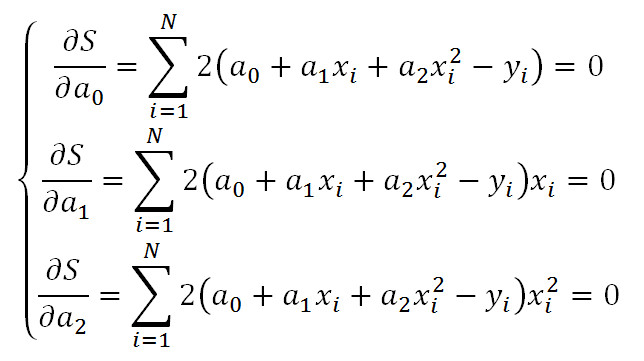
Получим систему уравнений:
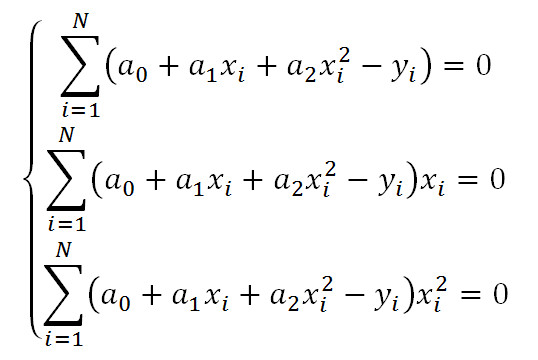
Выполним преобразования:
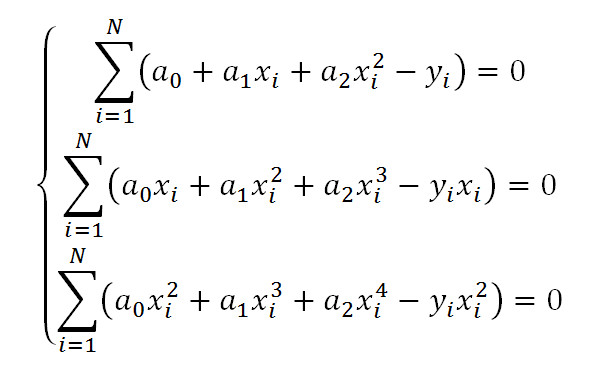
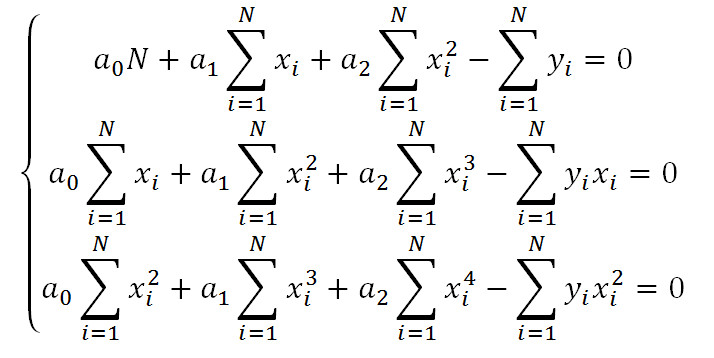
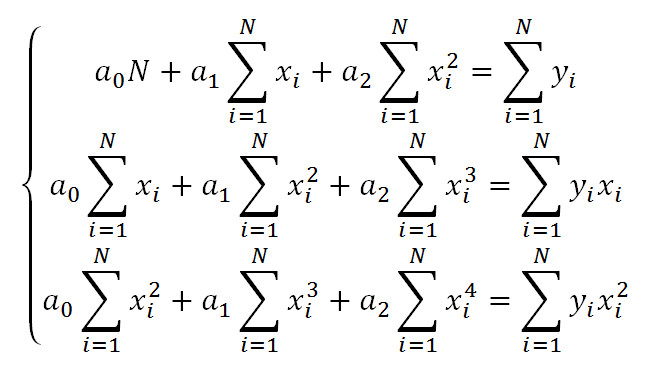
Введем обозначения:
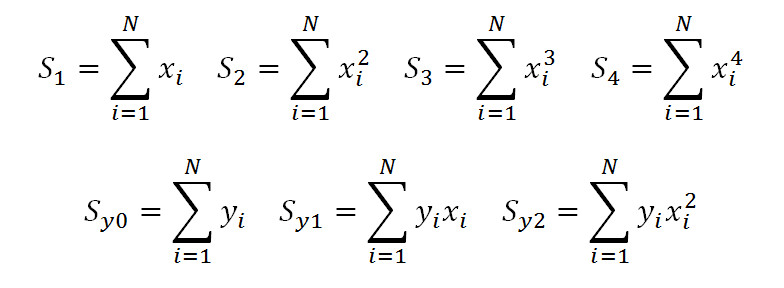
В результате система уравнений примет компактный вид:
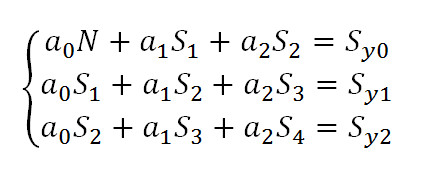
Эту систему уравнений можно записать в матричном виде:
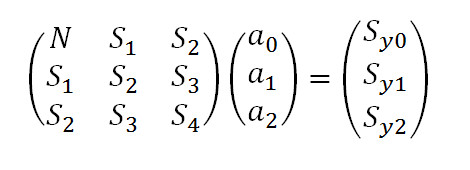
Решение системы уравнений в матричном виде имеет вид:

На этом все аналитические выкладки заканчиваются и можно перейти к вычислениям в Microsoft Excel.
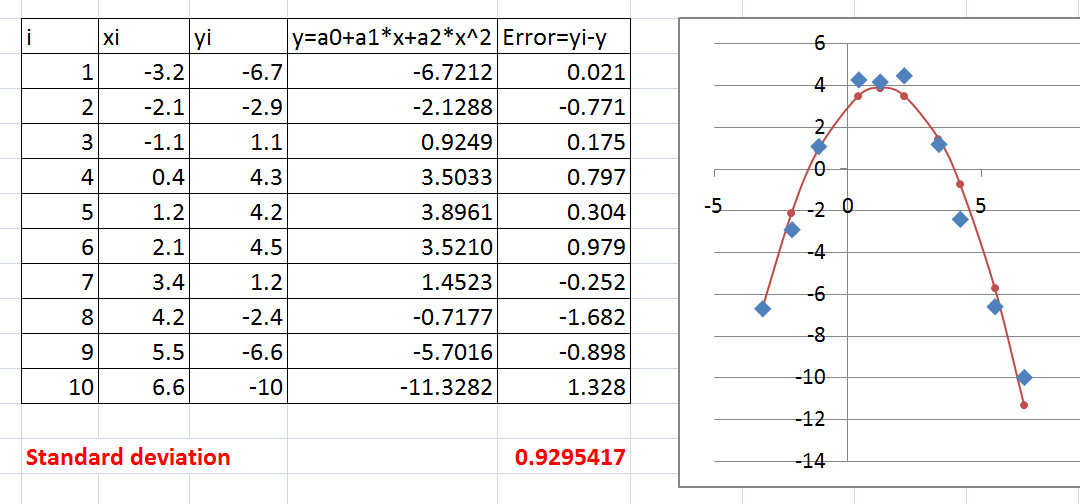
Готовый файл: LS.xls.
Подобные статьи: Как найти параметры прямой по результатам измерений?

1 комментарий на «Как найти параметры параболы по результатам измерений?»